
데이터 처리에서 가장 중요한 2가지 문제는 검색(search) 과 정렬(sorting) 이다. 이 중에서 데이터를 크기 순으로 정렬하는데 사용할 수 있는 알고리즘은 정말 많이 제안되었다. 그 중에서 가장 흔하게 활용되는 것이 셀렉션 소팅(Selection sorting)과 버블 소팅 (bubble sorting), 퀵 소팅 (Quick sorting), 바이너리 소팅 (Binary sorting) 등이다.
우선 가장 기본적인 선택정렬(selction sorting)을 먼저 다루어 보자.
○ 선택 정렬 (selection sorting)
보통 정렬의 이름에 그 정렬의 특징이 드러나는데, 선택정렬은, 예를 들어 오름차순이라면, 가장 큰 값을 "선택"하여 가장 마지막 값과 바꾸는 방식을 통해 데이터를 정렬하게 된다.
만약 정렬해야 할 데이터가 아래와 같다고 하자.

리스트에서 가장 큰 값을 찾는다. 현재 리스트에서는 9 값이 가장 크다. 그 값을 가장 마지막 값과 서로 바꾼다

그러면, 가장 마지막 자리에 있던 4 값이 원래 9가 있던 자리에 오고, 가장 큰 값인 9는 가장 마지막 자리로 옮긴다. 두개의 값이 서로 간에 자리를 바꾼다고 해서 이 과정을 스왑(swap)이라고 부른다.

이제 마지막 값은 정렬이 끝난 상태이다. 즉, 전체 9개 데이터 중 마지막 값은 정렬이 끝났고, 나머지 8개 데이터에 대한 정렬을 똑 같은 방법으로 다시 반복하면 된다.
즉, 정렬이 안되어 있는 부분의 데이터에 대해 가장 큰 값을 구한다. 현재로는 8이다. 이 값을 가장 마지막 값 (현재로는 5이다) 과 스왑하는 것이다. 이제, 마지막 2개의 값 8, 9는 정렬이 된 상태가 된다.

이런 과정을 계속 반복하면 정렬이 완성되게 된다.
그런데, 리스트의 최대 값을 구하여 마지막 값과 바꿀려면 최대값의 위치(인덱스)를 알아야 한다. 예를 들어, a[2] 값이 가장 큰 값이고 마지막 값이 a[8] 이라면 아래의 코드로 2개 값의 위치를 바꿀 수 있다. 이것이 스왑(swap) 코드이다.

실제, 두 값을 바꾼다고 하면 언뜻 떠오르는 코드는 아래와 같은 코드이다. #1에서 a[8] 값을 a[2] 변수에 저장하고, #2에서 a[2] 값을 a[8]에 저장하는 방법이다. 하지만, 이렇게 되면 #2에서 a[8]에 저장될 a[2]의 값이 #1에서 이미 a[8] 값으로 바뀐 다음이기 때문에 결국, a[2]와 a[8]이 하나의 값으로 같아져 버리는 문제가 생긴다.

실제로, 아래와 같이 코드를 실행해 보면, a[2]와 a[8]은 같은 값 4로 바뀌게 된다. 물론, 우리가 원하는 결과가 아니다.

왜 이같은 문제가 생겼나? 그것은 #1 에서 a[2] 값이 a[8] 값으로 바뀌기 때문이다. 그래서, 바뀌기 전에 다른 장소에 그 값을 복사해 두고, 나중에 a[2] 값이 필요할 때 그 값을 사용하는 것이다. 아래의 그림을 참고하기 바란다.
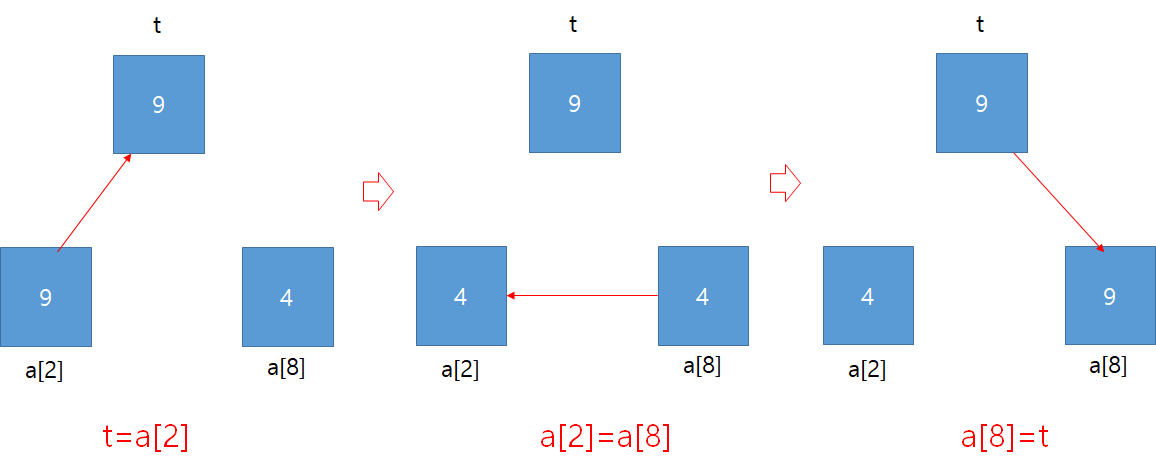
다시 원래대로 돌아가서, 이 같은 취지에서, 가장 큰 값을 구하는 것이 중요한 게 아니라 그 값이 저장되어 있는 인덱스 (즉, 가장 큰값을 저장하고 있는 변수 명) 을 찾는 것이 필요하다. 가장 큰 값의 인덱스를 찾는 코드는 아래와 같다. 우리가 [알고리즘 연습-2]에서 살펴본 최대값 구하는 알고리즘에서 #2, #4 코드만 추가된 형태이다.

우선, #1에서 제일 큰 값을 가리킬 변수 m 에 초기 값으로 a[0] 값을 저장하고 #2에서 m 값의 인덱스를 0 으로 초기화 했다. 그 다음 for-loop에서 현재까지 알고 있는 최대값인 m 값보다 큰 값이 나타나면 (if m<a[x]), m 값을 큰 값으로 바꾸어 주고, 그 값의 인덱스를 pos에 저장해 둔다(#3과 #4).
실제 루프를 끝내고 나면, m 변수에는 리스트 요소 값 중 가장 큰 값이, 그리고 pos에는 그 값의 인덱스 값이 저장되게 된다.
리스트에서 가장 큰 값을 찾고 나면, 이제 그 값과 가장 마지막 값을 서로 스왑해 주면 된다.
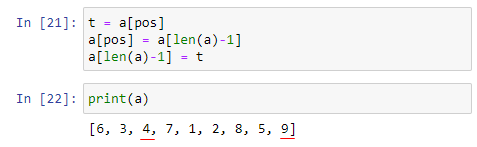
실제 전체 코드의 형태를 보면, 아래와 같다.
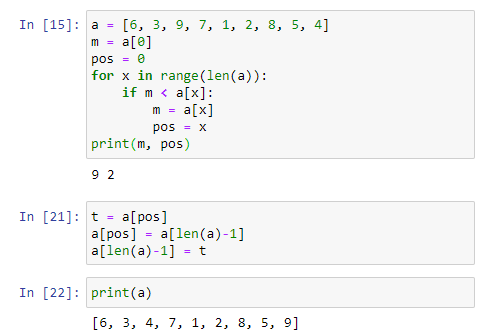
이제 뭐 하면 되나? 리스트의 마지막 값은 정렬이 되었으니, 나머지 값 즉, [6, 3, 4, 7, 1, 2, 8, 5] 에 대해서 동일한 과정을 반복하면 된다. 그 과정은 아래와 같다. 리스트의 마지막 2개의 값이 8, 9 로 정렬이 된 것을 확인하기 바란다.
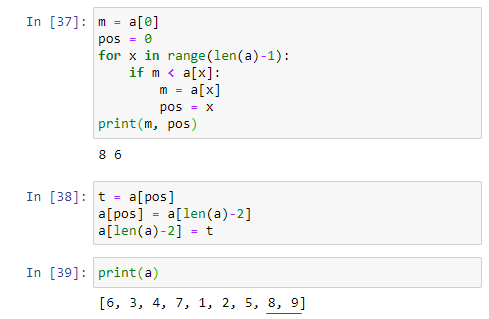
가장 큰 값인 9를 정렬하는 코드와 두번째로 큰 값인 8을 정렬하는 코드가 매우 비슷한 것을 확인할 수 있다. 뭐가 바뀌고 있나 확인해 보자. 반복인데, 무엇인가 바뀌면서 반복이다. For 루프와 반복변수를 떠올릴 수 있다면 문제는 끝이다.
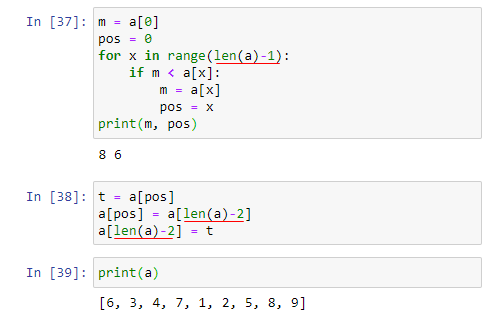
빨간색으로 언더라인된 부분만 다르다. In[37]에서 빨간색으로 언더라인된 부분이 9를 정렬할 때에는 len(a) 이었는데, 8을 정렬할 때에는 len(a)-1로 1만큼 작아졌다. In[38]에서는 len(a)-1 이었다가 len(a)-2로 1만큼 작아졌다.
그 다음에는 어떻게 바뀌면 될까? 이것을 for 루프로 만들어 보면 아래의 코드와 같다.

정렬이 진행되는 과정을 확인해 보기 바란다.
처음에는 많은 연습이 필요한 부분이다. 실제 코드를 만들면서 반복을 확인하고, 그 반복을 for-loop이나 while-loop로 만들고, 그리고 나서 실제로 내가 만든 for나 while 루프가 내가 만들려고 했던 반복을 잘 표현하고 있는지를 꼭 확인해 보기 바란다.
무슨 얘기다? 손으로, 연필로 루프를 따라가 보라는 뜻이다. 내가 만든 for 루프를 꼭 검증하는 습관을 들이기 바란다. 최소한, 처음에 공부할 때 만이라도. 나중에 익숙해지면 저절로 그림이 그려진다.
우선, k 값이 len(a) 일 때에는 위의 for-loop는 아래와 같이 동작한다. 우리가 처음에 만들어 본 가장 큰 값인 9를 정렬할 때 만들어 본 코드와 동일한지 확인하기 바란다.

그 다음으로 k 값이 len(a)-1 일때에, 8을 정렬하는 코드와 같은지 확인해 보기 바란다.
일반적으로 앞의 2가지 경우가 잘 맞으면 그 다음 부터도 잘 맞게 되어 있다. 단, 마지막 값만 확인해 보자. 우리 문제의 경우는 k 값이 1일 때이다.
k 값이 1이면 for-loop는 아래와 같이 작동한다.

어때 보이는가? k=0 이면 결국 a[0]에 들어갈 가장 작은 값을 구하는 것이 되는데, 앞의 정렬 단계에서 큰 값들을 스왚하다 보면 저절로 a[0]에 가장 작은 값이 저장되게 되어 굳이 반복할 필요가 없는 경우가 된다. for 루프를 for k in range(len(a), 1, -1) 로 하면 조금 더 빠르게 답을 낼 수가 있다는 뜻이다.
○ 버블 소팅 (bubble sorting)
** 버블소팅에 대한 내용은 [파이썬 알고리즘 객체지향 코딩의 기술]을 참고하기 바랍니다
'파이썬 (python)' 카테고리의 다른 글
| [python 25] 파이썬 1부, 알고리즘 편을 끝내며 (0) | 2020.05.07 |
|---|---|
| [python 24] 알고리즘 연습 - 4 : 두번째로 큰 값 찾기 (0) | 2020.04.25 |
| [python 22] 디버깅의 2가지 방법 (*작성중*) (0) | 2020.04.10 |
| [python 21] 사용자 정의 식별자와 참조 범위 (0) | 2020.04.10 |
| [python 20] 알고리즘 연습 - 2 (0) | 2020.04.01 |



